Back in the day, one of the most celebrated puzzles in the history of mathematics was Fermat’s Last Theorem. Middle school students can easily grasp the essence of this conundrum. Still, despite the attempts of legendary mathematicians over the ages, it remained unsolved for over 350 years. Today, we’ll break down the proof of Fermat’s Last Theorem in a way that even those who aren’t math enthusiasts can understand.
What’s Fermat’s Last Theorem?
In 1637, the mathematician Fermat scribbled down a problem in the margin of his book titled “Arithmetica.” This note came to be known as Fermat’s Last Theorem. It’s stated as:
For any value of \(n≧3\), the equation \(x^n+y^n=z^n\) has no natural number solutions.
On the surface, it might seem like a straightforward equation, reminiscent of trigonometric equations. But for around 350 years, multiple mathematicians grappled with its proof, only to come up short.
An intriguing tidbit: Alongside this problem, Fermat penned the now-famous words, “I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.” Fermat had a habit of jotting down problems, inspired by what he read, and then attempting to solve them in the margins of his books. Whether he genuinely had a proof for this theorem remains known only to Fermat himself.
A Historical Dive into the Proof of Fermat’s Last Theorem
It wasn’t until 1995 that Fermat’s Last Theorem was definitively proven, and that credit goes to Andrew Wiles. But before that groundbreaking moment, there was a lengthy history of brilliant minds across generations trying to solve this mathematical riddle.
1640: Fermat Himself
Fermat managed to prove his theorem for \(n=4\).
Note: It was Euler who found out that Fermat had inadvertently proven it for this value.
1753: Euler
Euler successfully proved the theorem for \(n=3\).
1823: Sophie Germain
Sophie claimed that if \(p\) is a prime and \((2p+1)\) is also a prime, then Fermat’s theorem probably holds true for \(n=p\). A noteworthy mention: Sophie Germain was a rare female mathematician during her era. With women denied formal education at that time, she is famously known to have disguised herself as a man to attend lectures.
1825: Dirichlet and Legendre
They proved Fermat’s theorem for \(n=5\).
1832: Dirichlet
Dirichlet went on to prove the theorem for \(n=14\).
1839: Lamé
Lamé established that Fermat’s theorem holds true for n=7.
An interesting side note: If one can prove the theorem for \(n=3\), it’s applicable for all multiples of 3. The reason is given by the equation \(x^{3n}+y^{3n}=z^{3n}\), which can be broken down as:
Let’s make a substitution:
\(x^n=X\)
\(y^n=Y\)
\(z^n=Z\)
\(X^3+Y^3=Z^3\)
Then, \(X^3+Y^3=Z^3\)
Given that \(X, Y,\) and \(Z\) are natural numbers, no natural numbers satisfy the equation:
Thus, if one can prove the theorem for every prime number, then Fermat’s Last Theorem would be proven for all values of \(n\). But here’s the catch: there are infinitely many prime numbers. So, it’s impractical to try proving it for each prime individually.
Wiles’ Triumph: Unraveling Fermat’s Last Theorem
Carrying the legacy of past mathematical giants, Andrew Wiles finally achieved a complete proof of Fermat’s Last Theorem. Now, the author admittedly struggled to fully grasp the intricate details of this proof, so we’ll be presenting an overview. For the detail-oriented among you, it’s worth noting that Wiles’ proof spans over 100 pages!
Transforming into an Elliptic Curve
First, Wiles transformed Fermat’s equation into an elliptic curve.
\(x^n+y^n=z^n\)
\(\displaystyle\frac{x^n}{z^n}+\frac{y^n}{z^n}=1\)
Now, let’s denote \(\displaystyle \frac{x}{z}=X\) , \(\displaystyle \frac{y}{z}=Y\)
So, \(X^n+Y^n=1\)
When substituting \(n≧3\) into this equation, it becomes an elliptic curve. A notable characteristic of elliptic curves is that they have only a finite number of rational points. A rational point refers to a point in space where all coordinate values are rational numbers (numbers that can be expressed as a fraction of two integers, \(a\) and \(b\)). This transformation means that, when considered as an elliptic curve, the solutions to Fermat’s Last Theorem are finite. With this, the problem of infinite prime numbers is addressed.
Freys’ Curve
Assuming for a moment that Fermat’s Last Theorem doesn’t hold, it would imply that at least one set of integer solutions exists. Let’s call these integers \(a, b,\) and \(c\). Since \(a, b,\) and \(c\) are solutions to Fermat’s equation, they possess the following attribute:
\(a^n+b^n=c^n\)
Now, let’s contemplate an elliptic curve, known as Frey’s curve, which incorporates these integers \(a, b,\) and \(c\):
\(y^2=x(x-a^n)(x+b^n)\)
*Note: This Frey’s curve lacks modularity when \(a^n+b^n=c^n\) has solutions that fulfill \(abc≠0\).
Furthermore, Frey’s curve is semi-stable. Meaning, if we assume Fermat’s Last Theorem doesn’t hold, Frey’s curve becomes a semi-stable elliptic curve that lacks modularity. Concepts like modularity and semi-stability are indeed complex. For now, just understand that such phenomena exist in the world of mathematics.
The Taniyama-Shimura Conjecture
Two Japanese researchers claimed that every elliptic curve defined over all rational number fields is modular.
Interestingly, the proof of the Taniyama-Shimura Conjecture came after Fermat’s Last Theorem was proven. However, this conjecture provided a significant hint towards the proof of Fermat’s Last Theorem.
Wiles’ Triumph
Andrew Wiles proved that “for semi-stable elliptic curves, the Taniyama-Shimura Conjecture holds true.” This was the final piece to the puzzle of Fermat’s Last Theorem. With this, we can say, “semi-stable elliptic curves are modular.”
Remember the Frey curve? It was described as “an elliptic curve that’s semi-stable but not modular.” However, since semi-stable elliptic curves should be modular, it implies that the Frey curve doesn’t exist.
The Frey curve was based on the premise that the equation \(x^n+y^n=z^n\) has at least one solution (when \(n≧3\)). If the Frey curve doesn’t exist, then the equation \(x^n+y^n=z^n\) doesn’t have any solutions for \(n≧3\).
In simpler terms, Fermat’s Last Theorem stands true. That’s how Fermat’s Last Theorem was finally proven. I hope you got the gist of it, even if it’s just a brief overview!
Proof via the ABC Conjecture
In April 2020, Professor Mochizuki from Japan provided a proof for the “Strong ABC Conjecture.” With this conjecture, proving Fermat’s Last Theorem becomes considerably more straightforward. Let’s briefly discuss the Strong ABC Conjecture.
The Strong ABC Conjecture is defined as:
For co-prime natural numbers \((a, b, c)\) that satisfy \(a+b=c\), the inequality \(c<rad(abc)^2\) holds true.
Co-prime numbers don’t have any common factors except for 1. For instance, 2 and 3 are co-prime, but 2 and 4 aren’t. \(rad(abc)\) signifies the product of distinct prime factors of \((a, b, c)\).
To better understand, consider the co-prime numbers \(a=7, b=9,\) and \(c=16\):
\(c<rad(abc)^2\)
\(16<rad(7×9×16)^2\)
\(16<rad(7×3^2×2^4)^2\)
\(16<(7×3×2)^2\)
\(16<1764\)
Thus, for \(a=7, b=9,\) and \(c=16\), the ABC Conjecture is satisfied. Now, let’s use this concept to prove Fermat’s Last Theorem!
Proof of Fermat’s Last Theorem
Assume the following holds for co-prime natural numbers \((x, y, z)\) and natural number \(n (n≧3)\):
By applying the Strong ABC Conjecture to \((x^n, y^n, z^n)\), we get:
\(c<rad(abc)^2\)
\(z^n<rad(x^ny^nz^n)^2\)・・・①
As \((x, y, z)\) are co-prime,
\(rad(x^ny^nz^n)^2=(xyz)^2\)・・・②
Given the relationships:
\(x<z\)
\(y<z\)
We deduce:
\(xyz<z^3\)・・・③
Combining equations ①, ②, and ③:
\(z^n<(xyz)^2<(z^3)^2\)
\(z^n<z^6\)
This proves that for any co-prime natural numbers \((x,y,z)\) satisfying \(x^n+y^n=z^n\), \(n\) must be less than 6.
Next, even for non-co-prime natural numbers \((x,y,z)\) satisfying:
\(x^n+y^n=z^n\)
If \((x, y, z)\) aren’t co-prime, they share common factors. Thus, they can be represented as:
\(x=ms\)
\(y=mt\)
\(z=mv\)
(Note: \((s,t,v)\) are co-prime.)
Substituting these into the equation:
\({ms}^n+{mt}^n={mv}^n\)
\(s^n+t^n=v^n\)
As \((s,t,v)\) are co-prime, combinations of \((s,t,v)\) satisfying the above are only for \(n<6\). This means that even for non-co-prime \((x,y,z)\), the equation \(x^n+y^n=z^n\) holds true only for \(n<6\).
Thus, for all natural numbers, Fermat’s Last Theorem holds true for \(n>6\). With cases \(n=3, 4\), and \(5\) already proven, Fermat’s Last Theorem is entirely proven. Compared to Wiles’ proof, this approach is quite intuitive!
Recommended Readings
For those interested in delving deeper into Fermat’s Last Theorem, I have some recommended literature for you.
While this article provided an explanation of the proof of Fermat’s Last Theorem, the allure of the theorem doesn’t stop there. Over 350 years, brilliant mathematicians have faced both failure and success in trying to solve this riddle. It’s an incredibly dramatic journey. The recommended book is a documentary that recounts the story leading up to Wiles’ complete proof. Given its narrative-driven content, it’s suitable for middle and high school students and even those with a background in humanities or liberal arts.


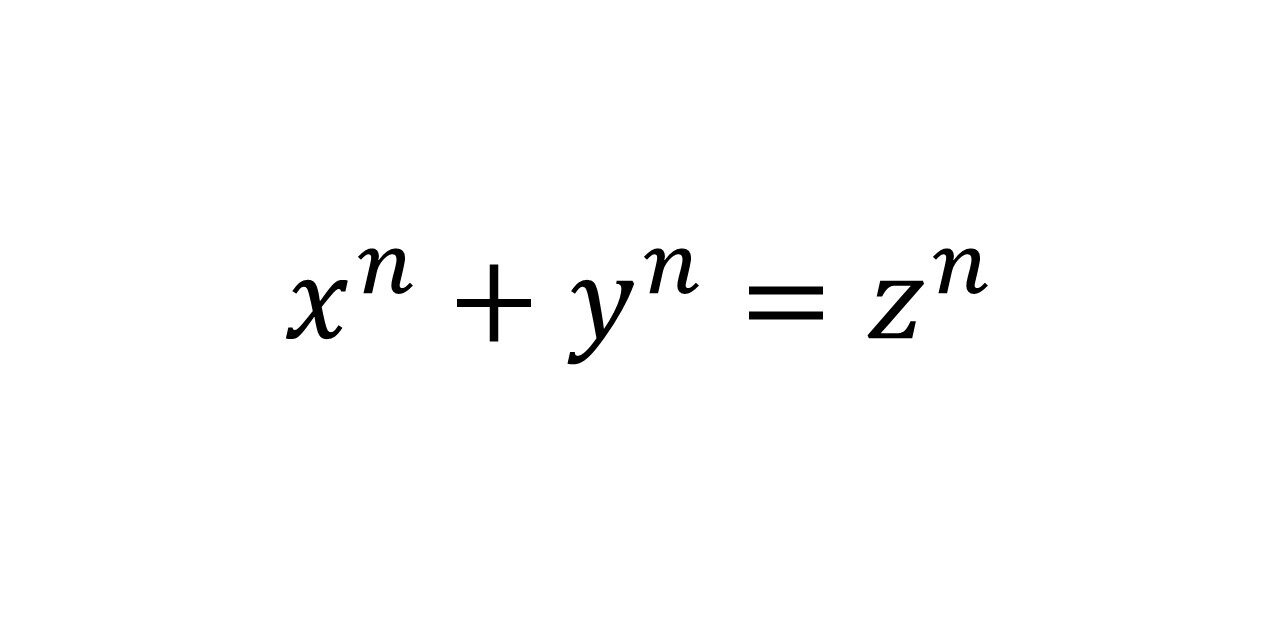



1 Comment