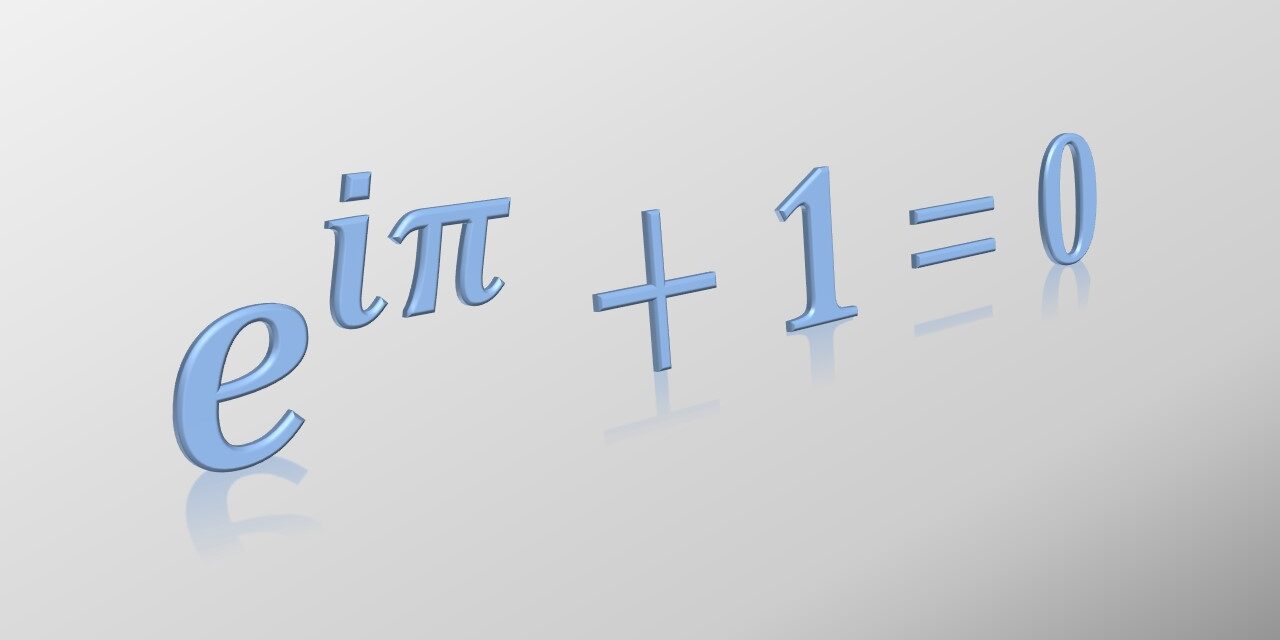Euler’s equation is famously known as the most beautiful formula in the world. However, many may find its beauty elusive. This article aims to demystify Euler’s formula for those without a background in mathematics. By the end, you may just find yourself trembling at the sheer elegance of Euler’s equation.
Euler’s Equation Explained
Here is Euler’s equation:
\(e^{iπ}+1=0\)
It’s touted as the most beautiful equation in the world. To appreciate the beauty of Euler’s equation, one must understand the concepts of pi (\(π\)), the natural logarithm base (\(e\)), the imaginary unit (\(i\)), and exponentiation. Don’t worry; we will explain each of these terms in a simple way, step by step.
What is Pi?
Let’s start with pi. You’ve probably heard of it before. Pi is the ratio of a circle’s circumference to its diameter, denoted by the symbol \(π\). For example, the circumference (\(C\)) of a circle with diameter (\(d\)) can be calculated as:
\(C=π×d\)
The value of pi is approximately:
\(π=3.14159265359 \cdots \)
To date, it has been calculated to more than two hundred billion digits and still shows no sign of ending.
The History of Pi
The use of pi dates back to around 2000 BCE, making it a number with a rich history.
The Natural Logarithm Base (e)
Next is the natural logarithm base, or \(e\). The number e is the sum of the inverses of all natural numbers to infinity and is represented by the symbol \(e\). It is calculated as:
\(\displaystyle e= \lim_{n \to +\infty} (\frac{1}{1}+ \frac{1}{n})^n \)
Like pi, the calculation of e is endless:
\(e=2.71828182845904523536 \cdots \)
You might wonder what use e has. For instance, the function e^x remains the same after differentiation, which is just one of its many unique properties. While it might not seem relevant to everyday life, it plays a crucial role in mathematics, especially in the fields of calculus and analysis.
Interestingly, using the number e can even increase your chances of making the optimal choice in certain decision-making scenarios, like selecting the best partner to marry.
The History of e
The number \(e\) was first approximated by John Napier in 1618.
Imaginary Unit (i)
The third concept is the imaginary unit, \(i\). It is defined as the value whose square is -1:
\(i^2=-1\)
Squaring a number means multiplying it by itself. A positive number squared is positive, and so is a negative number squared; zero squared is zero. Hence, any real number squared results in a positive outcome or zero. This means the imaginary unit \(i\) represents a value beyond our usual comprehension.
The History of Imaginary Numbers
The concept of imaginary numbers began to be used around the 17th century, attributed to René Descartes.
Understanding Exponents
An exponent refers to the ‘n’ in \(x^n\). For example, \(2^3\) means multiplying 2 by itself three times, which is calculated as follows:
\(2^3=2×2×2=8\)
But what about \(2^{0.5}\) or \(2^{-1}\)? Do you think they can’t be calculated? In fact, they can:
\(2^{0.5}=\sqrt{2}\)
\(2^{-1}=0.5\)
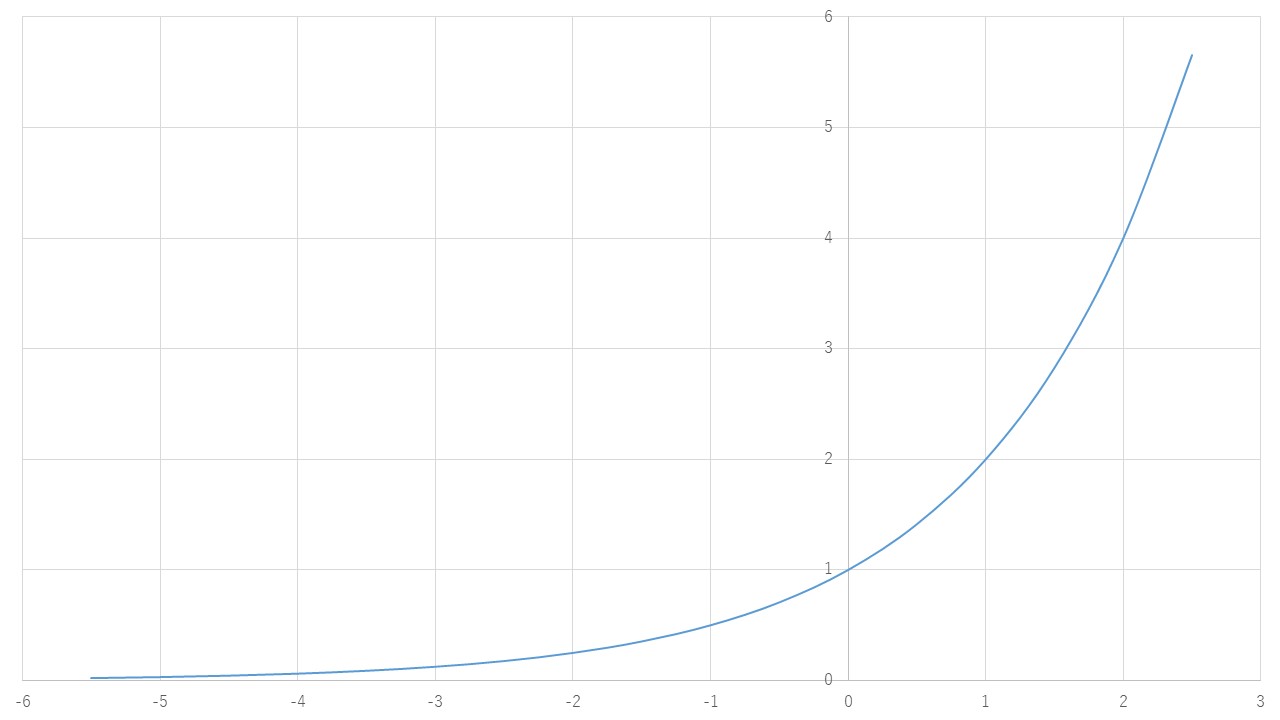
The graph of \(x=2^n\) looks like this. The fact that we can graph it shows that we can compute exponents that are not just whole numbers, but also fractions and negative numbers.
The Most Beautiful Equation in the World
In 1748, Euler made a discovery. In the 17th century, the concept of the imaginary number \(i\), a number beyond our previous recognition, was defined. It was to be multiplied by the number \(π\), an infinite number discovered around 2000 BCE.
\(πi\)
Then, the number \(e\), discovered in 1618 and also an infinite number, is raised to the power of \(πi\):
\(e^{πi}\)
At first glance, this expression seems impossible to calculate:
\(e^{πi}=(2.71・・・)^{(3.14・・・)×\sqrt-1}\)
However, by adding 1 to this formula, as if by magic, it simply becomes 0.
\(e^{iπ}+1=0\)
It’s like untangling a complicated knot with just a flick of the finger. That is Euler’s equation. It’s so beautiful it’s exhilarating.
Conclusion
This explanation has been kept simple, aimed at those not very familiar with mathematics. If you found this topic inspiring, why not learn about Euler’s life as well? His life was as rich and beautiful as the equation that bears his name.