How Likely is it to Get 50 Heads in 100 Coin Tosses?

Ever tossed a coin and thought about the odds? If I asked you the chances of getting heads exactly 50 times in 100 coin tosses, would you instinctively say 50%? You’re not alone. But, spoiler alert: that’s not the right answer. And no, we’re not using a trick coin here.

The Surprising Odds of Landing 50 Heads in 100 Tosses

You’d think it’s a straightforward math problem. Toss a coin 100 times, and since both heads and tails have an equal 50% chance of landing, you’d get heads 50 times, right? Well, not quite.

Brace yourself – the actual odds of this happening are around 8%. A bit shocking, right? The catch is we’re looking for the exact number, 50 times. So, even getting heads 49 or 51 times can significantly affect this probability.

How Do We Calculate That?

To get the 8% figure for the heads popping up 50 times out of 100, we use the following formula:

\(\displaystyle P={}_{100} \mathrm{C}_{50} ×(\frac{1}{2})^{100}\)
\(\displaystyle P=\frac{100!}{50!×50!} ×(\frac{1}{2})^{100}\)
\(\displaystyle P=0.079589≒8%\)

What If We Change the Number of Tosses?

You might wonder: what happens if we change the number of coin tosses? Does the probability of getting heads exactly half the time remain the same? Below is a table with results:

 

Number of Tosses	Probability of Getting Heads Exactly Half the Time
2	50％
10	25％
50	11％
100	8％
170	6％

 

This graph showcases how the odds change based on the number of coin tosses:

 

 

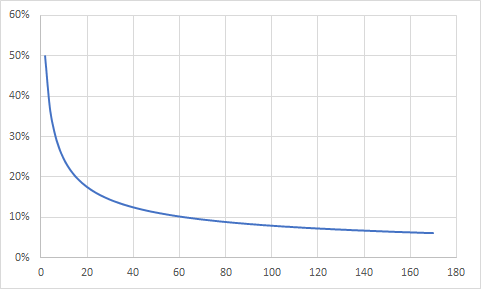
Starting with a 50% chance for a single toss, the probability decreases as we increase the number of tosses. Turns out, getting a perfect half-and-half outcome is trickier than you might think!