Ever stumbled upon a puzzle that’s so clear-cut yet impossible to explain? Dive into this mind-boggling mathematical mystery.
Ever Heard of the Envelope Trick?
So, there were these two good Samaritans, let’s call them Alex and Bob. One day, they spotted an elderly lady struggling with some heavy luggage. Being the kind-hearted souls they are, they rushed over to help her out. In gratitude, the old lady decided to give them a little cash reward, but with a twist.
She said, Inside these two envelopes are checks for your reward. But there’s a catch. One envelope contains ten times the amount of the other!
Alex thought, Let’s say my envelope has $10. That means Bob’s could either have $1 or $100. With a 50/50 chance, if I were to swap, the expected gain would be…
\(\displaystyle \frac{1+100}{2}=50.50\)
In short, I could either have $10 now or an expected $50.50 if I swapped. Definitely worth a trade!
Bob had the same idea and wanted to swap too. But can both really profit from the trade? Is it possible that simply trading envelopes can increase money? This paradox hasn’t been entirely resolved, and opinions still vary.
Two Ways to Think About It
There are a couple of schools of thought on this issue.
Adjusting Probability Perspective
Rethinking the 50% chance for either $1 or $100 might be the way. Given the different distances from $10 to both $1 and $100, it’s suggested that weights be added to the probabilities during calculations.
Probability for $1: \(\displaystyle \frac{100-10}{100-1}= \frac{10}{11}\)
Probability for $100:\(\displaystyle \frac{10-1}{100-10}= \frac{1}{11}\)
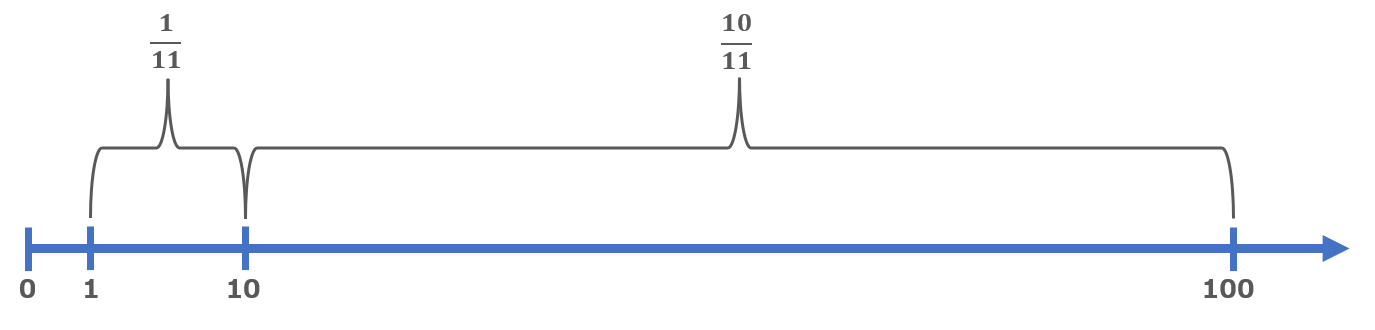Thus, the expected gain:\(\displaystyle 100× \frac{10}{11}＋100× \frac{1}{11}＝10\)
When calculated this way, the expected gain matches the original $10, making things coherent.
<h3>Shifting the Expected Value Concept</h3>
Instead of focusing on the gains from swapping, consider the expected reward from the elderly lady. For instance, if one envelope has $10, the expected reward ‘K’ is calculated as:
\(\displaystyle K= \frac{121}{2}\)
\(\displaystyle K＝60.50\)
Meaning, regardless of the trade, the expected amount you’d get from the lady is $60.50.
If you’re a student, popping this question to your math teacher might spice up your class time. Give it a shot!
Discover Famous Math Theories: Intriguing Number Facts and Mathematics Tricks That Will Amaze You
You know how math classes in school can be kinda dull or even a pain for most folks, right? But get this, math is actually pretty fascinating. To prove how cool math can be, I’ve gathered some fun math stories for you! Even if you’re not a math fan, you’re gonna have a good time…
