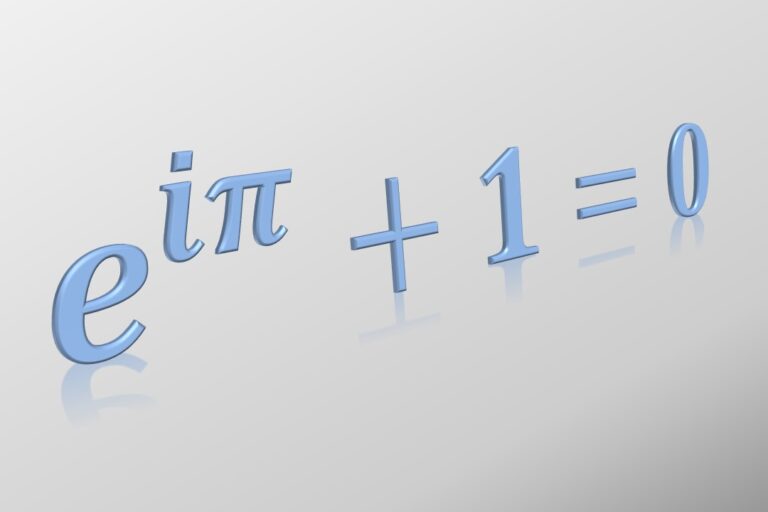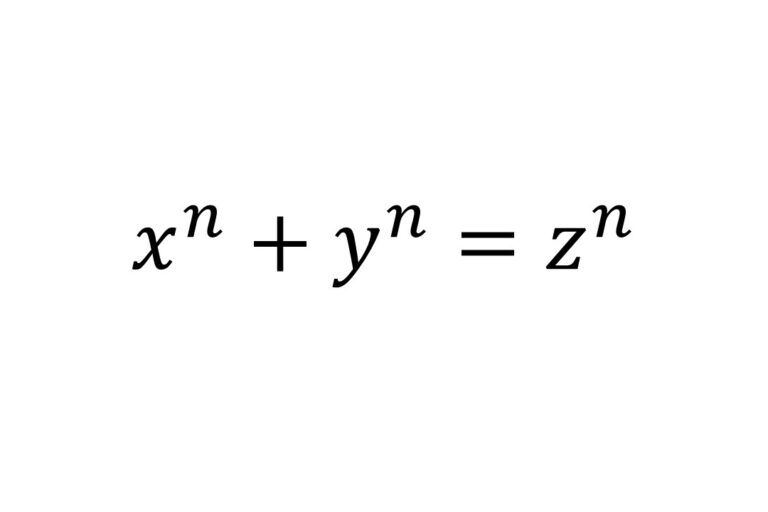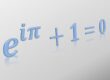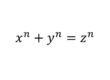Just as naturally as a person breathes or an eagle soars through the skies without apparent effort, the genius mathematician Leonhard Euler was said to solve mathematical puzzles. But why is Euler regarded as a genius? In this article, we will dive into some incredible stories about Euler that will undoubtedly leave you in awe of his brilliance.
The Early Life of Euler
Born in 1707 as the son of a pastor, Euler showed extraordinary mathematical talent from a young age. However, his father, devoted to the church, desperately wanted Euler to pursue theology. It was the intervention of the renowned Bernoulli family—celebrated as the greatest mathematical lineage of the time—that set Euler on his path to becoming a mathematician. The Bernoulli’s recognition of Euler’s talents was fortuitous indeed.
Euler’s Era
As the 18th century dawned, mathematics began to be recognized as a useful discipline, thanks in part to the achievements of Sir Isaac Newton—the man who conceived the notion of gravity from an apple’s fall. Newton’s application of mathematics to the natural world, calculating trajectories of cannonballs, amongst other things, was pivotal in validating the field. Before this, mathematicians were often thought to simply play with puzzles. Euler was born into an era where mathematics started gaining its due recognition.
Europe’s power brokers would task Euler with solving various complex problems, and the brilliant Euler solved them all, contributing to advancements in navigation, economics, and acoustics.
Tales of Euler’s Wit
When Euler’s reputation for solving any problem became widespread, a philosopher challenged him to prove the existence of God—a task meant more out of spite than genuine inquiry. Euler’s response was:
\(\displaystyle \frac{a+b^n}{n}=x\) therefore, God exists.
Confused? The equation is actually nonsense. However, no one could dare to contradict Euler, who had solved every challenge presented to him, and the philosopher left without a word. Euler also had a sense of humor.
Euler’s Tragedy
In 1735, the Paris Academy set a prize for solving a complex astronomical problem. Many famous mathematicians found it too daunting and believed it couldn’t be solved within the Academy’s deadline. Euler was different. He worked non-stop for three days, and his relentless effort paid off with a solution, winning him the prize. However, the poor conditions and intense stress cost him the sight in one eye.
Losing his vision to such dedication is unimaginable, yet Euler remained undeterred, claiming it helped him concentrate better.
Another Stroke of Misfortune
Tragedy struck again when Euler’s remaining eye was afflicted with cataracts. Despite this, he trained himself to write with his eyes closed before he lost his sight completely.
Euler possessed an extraordinary ability to perform calculations in his head and remember almost everything he read. Using these unique skills, he continued to create mathematics for 17 years after becoming blind. Remarkably, it was after losing his sight that Euler achieved the unprecedented feat of calculating the orbit of the moon—a testament to his incredible genius.
Euler’s Contributions
The genius of Euler is evident through his numerous contributions. Among the most famous is the discovery of Euler’s formula, often hailed as “the most beautiful equation in the world.” For more on Euler’s formula, please refer to this article.
Euler’s Contributions
The genius of Euler is evident through his numerous contributions. Among the most famous is the discovery of Euler’s formula, often hailed as “the most beautiful equation in the world.” For more on Euler’s formula, please refer to this article.
Euler and Fermat’s Last Theorem
Even a mathematician of Euler’s caliber encountered problems that were insurmountable at the time. One such challenge was Fermat’s Last Theorem, which states:
There are no natural number solutions to the equation \(x^n+y^n=z^n\) for any integer value of \(n\) greater than 2.
Fermat’s Last Theorem, posited by the 17th-century mathematician Pierre de Fermat, remained an enigmatic super-problem for about 350 years until its proof was finally established. Euler was unable to solve the theorem entirely, but his role in its history is far from insignificant. He was the one who took the crucial first steps towards its eventual solution.
It was Euler who proved that Fermat’s Last Theorem held true for the case when n equals 4. He made this discovery while reading “Arithmetica,” where he noticed that Fermat had clandestinely provided a proof for this special case.
Building on this, Euler sought to prove the theorem for all natural numbers greater than 3. He succeeded in proving it for the case when n equals 3 by cleverly combining the method of infinite descent with complex numbers.
Yet, that was as far as Euler could go. The final resolution of Fermat’s Last Theorem, an enigma that even the astonishingly talented Euler could not fully decipher, is detailed in another article.