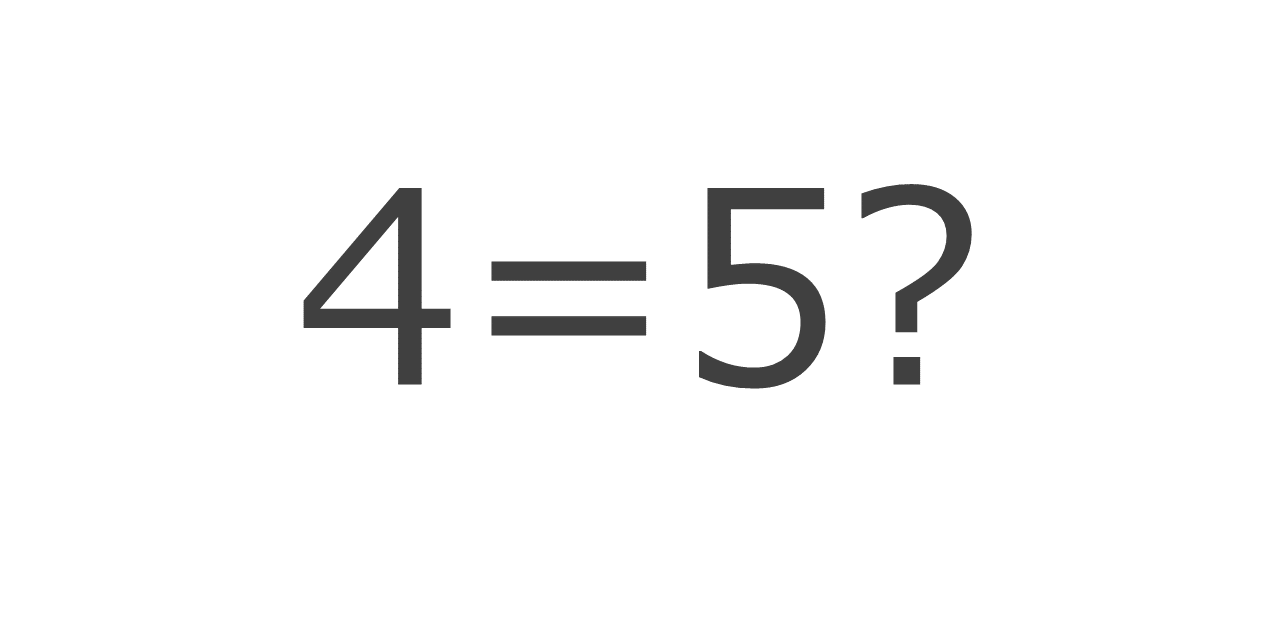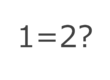Ever thought 4 could equal 5? Let’s dive deep into two proofs and see if you can find the error!
Proof 1: A Dive into Basic Arithmetic
So, we’re given a basic arithmetic challenge that tries to prove 4=5. Can you spot the mistake?
\(20-20=25-25\)
\((5×4)-(5×4)=(5×5)-(5×5)\)
\(4×(5-5)=5×(5-5)\)
\(4=5\)
\(2+2=5\)
Mistake Breakdown:
Alright, let’s clear things up. The hiccup happens here:
\(4×(5-5)=5×(5-5)\) leading to \(4=5\)
Remember, 5-5 is 0. And in math, multiplying by zero always equals zero. This proof falls apart right there. We avoid dividing by zero in math for this very reason.
Proof 2: Bringing in Middle School Math
Leveling up! Using middle school math, we’ll attempt to prove 4=5 once again. Can you catch the error this time?
\(-20=-20\)
\(16-36=25-45\)
\(4^2-4×9=5^2-5×9\)
\(\displaystyle 4^2-2\left(4×\frac{9}{2}\right)=5^2-2\left(5×\frac{9}{2}\right)\)
\(\displaystyle 4^2-2\left(4×\frac{9}{2}\right)+\left(\frac{9}{2}\right)^2\\ \displaystyle=5^2-2\left(5×\frac{9}{2}\right)+\left(\frac{9}{2}\right)^2\)
\(\displaystyle \left(4-\frac{9}{2}\right)^2=\left(5-\frac{9}{2}\right)^2\)
\(\displaystyle 4-\frac{9}{2}=5-\frac{9}{2}\)
\(\displaystyle 4=5\)
Mistake Breakdown:
Let’s uncover the mistake:
\(\displaystyle \left(4-\frac{9}{2}\right)^2=\left(5-\frac{9}{2}\right)^2\) leading to \(\displaystyle 4-\frac{9}{2}=5-\frac{9}{2}\)
When taking square roots, there’s a twist: if \(a^2=b^2\), then \(a\) could be \(b\) or \(-b\). This proof only considered one possibility. Had we tried the other:
\(\displaystyle 4-\frac{9}{2}=-\left(5-\frac{9}{2}\right)\)
\(\displaystyle \left(\frac{8}{2}-\frac{9}{2}\right)=-\left(\frac{10}{2}-\frac{9}{2}\right)\)
\(\displaystyle -\frac{1}{2}=-\frac{1}{2}\)