Unlocking the Mystery of the Fourth Dimension: The Magic of the Tesseract Explained

Ever wondered if it’s possible to visualize a four-dimensional shape? It turns out, there’s something called a “Tesseract” which does just that. In this blog post, we’ll walk you through the art of drafting a 4D shape and give you a sneak peek into the world of the Tesseract.

How to Draw Shapes in Different Dimensions

Before diving deep into the 4D, let’s quickly recap how to draft in one, two, and three dimensions. Stick with me—it’s simpler than you think!

1D Drafting

One dimension looks something like this:

It’s pretty straightforward—just a line. It can only go in one direction.

2D Drafting

Next up, we have two dimensions. Think of a square.

What differentiates a line (1D) from a square (2D)?

• The number of vertices doubles (from 2 to 4).
• From every corner, there are two lines stretching out at right angles.

Remember these differences; they’re essential for understanding the Tesseract.

3D Drafting

Now, visualize a cube for three dimensions.

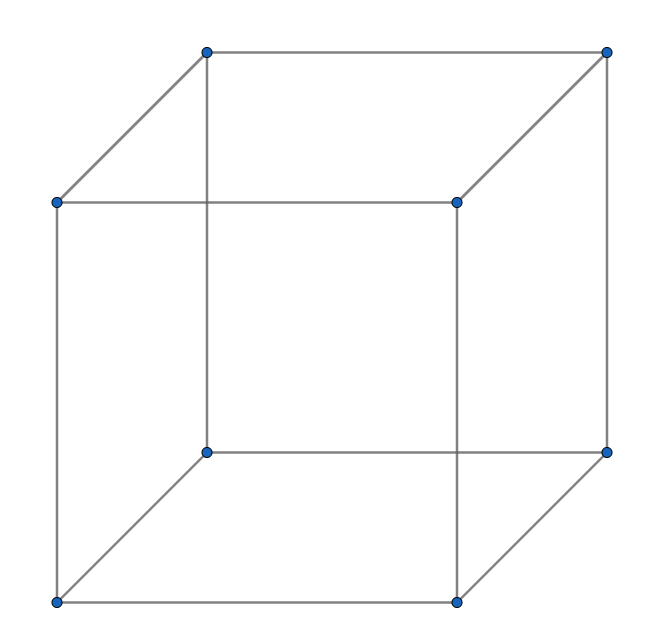
Comparing a square (2D) to a cube (3D):

• The number of vertices doubles again (from 4 to 8).
• Every vertex now has three lines emerging at right angles.

Starting to see a pattern? Now onto the main event!

Drafting a 4D Shape: Meet the Tesseract

Applying the same logic, here’s how a Tesseract differs from a cube:

• Vertex count doubles yet again (from 8 to 16).
• From every point, four lines radiate at right angles.

Check out the Tesseract we’ve sketched here:

Source: wikipedia

It might look like a cube within a cube at first. Think that’s all? Wait till you see it in action!

Source: wikipedia

The Tesseract has this uncanny ability to move in mind-bending ways because each vertex connects with four other lines at right angles. With a touch of math magic, we can represent this 4D wonder even in our 3D world.