Maximizing Love: How Math Can Boost Your Chances of Finding The Ideal Partner

Ever felt the dilemma of whether the person you’re dating is truly the best match for you? Maybe there’s someone even better waiting out there? Dive deep into this piece as we use math to boost your chances of walking down the aisle with your ideal partner.

Increase Your Odds: A 37% Chance to Marry Your Perfect Match!

Let’s play with an idea: You date 100 different people during your lifetime. Here’s the twist: propose to anyone, and they’ll nod a yes. But, only one date at a time, and if you part ways, no U-turns allowed.

Relying purely on luck, your shot at picking the top partner stands at a bleak 1%. However, apply some clever math, and those odds soar to a whopping 37%. That’s right, about 1 in 3 can end up with their numero uno using this tactic!

Skip the Initial 37

Here’s the trick: out of the 100, you bypass the initial 37. Starting from the 38th, if you come across someone who outshines all the previous 37, it’s time to pop the question. This approach gives you a 37% shot at winning the love jackpot.

Now, real talk: dating 100 folks might sound like fiction. So, if you’re thinking of settling between ages 20 and 29, perhaps don’t even think of commitment until 24. From that point, if someone tops everyone you’ve dated before, say the magic words!

But hold on, there’s a caveat: while 37% might find their dream match, about 26% may have to settle for second best (or lower) and a risky 37% might never hear the wedding bells. No matches post the 37 could mean your soulmate was among the initial lot.

The Logic Behind the Love

Ready for a bit of math magic?

Suppose you’ll encounter \(n\) potential partners in your life. You’ll bid goodbye to the first \(x\) without a second thought. From the \(x+1\) individual onwards, if they shine brighter than all before them, you commit. Now, the probability of this strategy succeeding, denoted as \(P(x)\), peaks at 37% when \(\displaystyle \frac{x}{n}\) is approximately 0.37.

To understand this, consider if the best partner was the \(m\)th person. If \(m≤x\), you’d definitely miss out on them, making the probability 0. Thus, only cases where \(m＞x\) are worth considering.

Given that any specific person being the best partner is \(\displaystyle \frac{1}{n}\), and the probability of a person better than all the first \(x\) but worse than the best one appearing before the \(m\)th person is \(\displaystyle \frac{x}{m-1}\), the overall probability \(P(x)\) is:

\(\displaystyle P(x)=\frac{1}{n}\sum_{m=x+1}^{n}\frac{x}{m-1}\)
\(\displaystyle P(x)=\frac{x}{n} \left( \frac{1}{x}+\frac{1}{x+1}+…+\frac{1}{n-1} \right)\)

For large \(n\), using Maclaurin series expansion, we get:

\(\displaystyle P(x)=\frac{x}{n}\log\frac{n}{x}\)

Plotting this for \(n=10\).

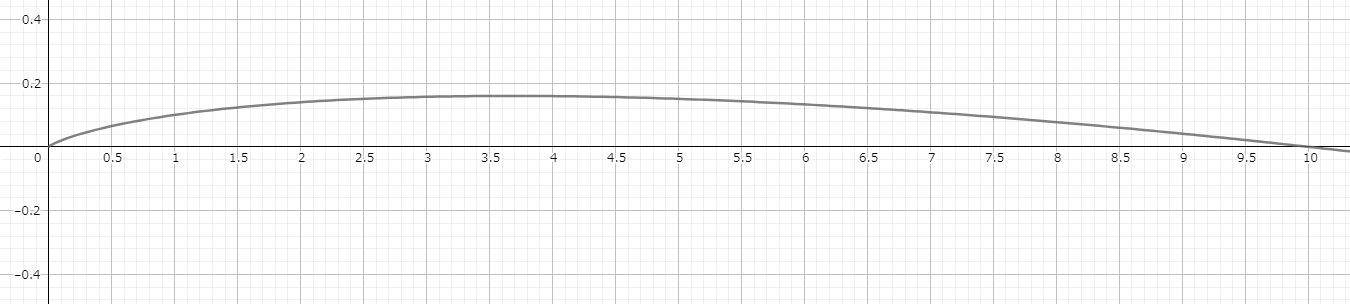
You’d see where \(P(x)\) maximizes. The point where the derivative \(P'(x)\) is zero gives:

\(\displaystyle P'(x)=\frac{x}{n}\log\frac{n}{x}-\frac{1}{n}\)

Setting \(P'(x)=0\), you’d find:

\(\displaystyle x=\frac{n}{e}\)

Breaking it down,\(\displaystyle \frac{n}{x}\) lands around 0.37, and \(P(x)\) at this juncture also hovers close to 0.37 or 37%.

And there you have it, math spicing up your romantic endeavors!