Ever been curious about what happens when you turn math into art? Sometimes, equations that look super complex end up producing the most fascinating and recognizable shapes when graphed. And if you can guess the shape from the equation, you might just be a math genius!
The Heart Equation
Let’s kick things off with a little love. Check out this equation:
\(\displaystyle x^2+(y-\sqrt[3]{x^2})^2=1\)
Graph it, and you’ll see:
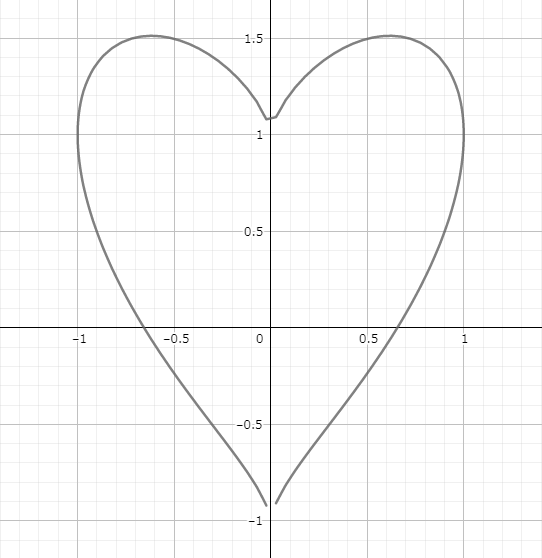
It’s popularly known as The love formula. So, if you get a random message from someone special with this equation, they’re definitely dropping a hint.
Filled-In Heart
But there’s more heart magic to unveil. Dive into this equation:
\(\displaystyle y=x^{\frac{2}{3}}+\frac{4}{5}\sqrt{\frac{9}{10}-x^2}\sin{100πx}\)
And the graph? Well:
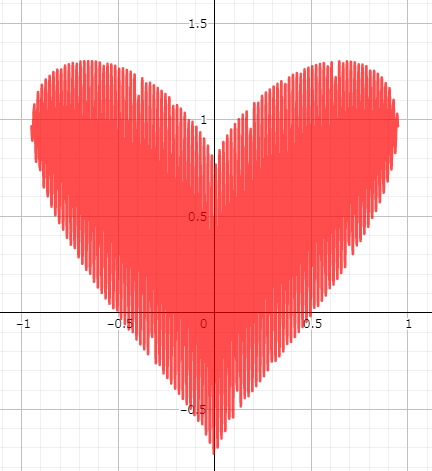
With those colors, it surely feels like love’s really in the air.
The Infinite Heart
For those out there who believe in endless love, here’s your equation:
\(y=\sqrt{|\sin{x}|}+\sqrt{|\cos{x}|}\)
\(y=\sqrt{|\sin{x}|}-\sqrt{|\cos{x}|}\)
Behold its graph:
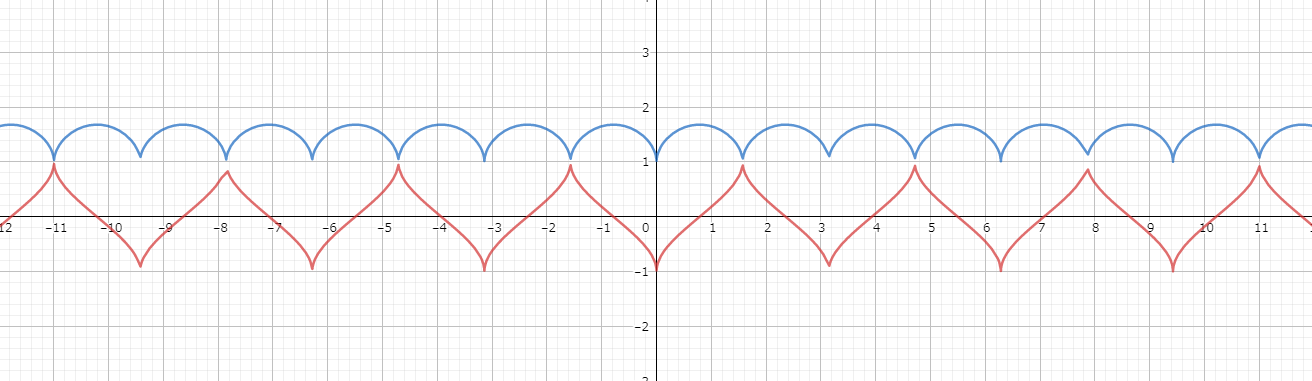
This heart goes on forever, symbolizing boundless affection.
Clover Equations
Shifting gears, let’s dive into clover equations.
3-Leaf Clover
Starting off with the classic three-leaf:
\(r=1+\cos{3θ}\)
Visualize:
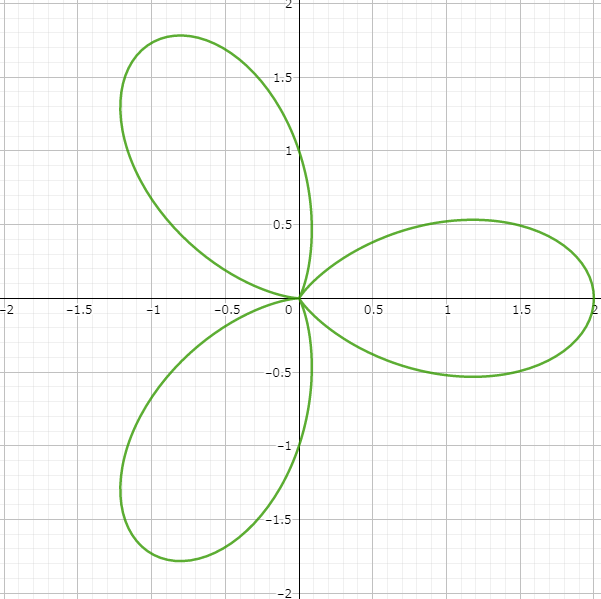
Note: This one’s in polar coordinates with variables r and θ.
4-Leaf Clover
Next, the four-leaf version:
\(r=1+\cos{4θ}\)
Here’s how it looks:
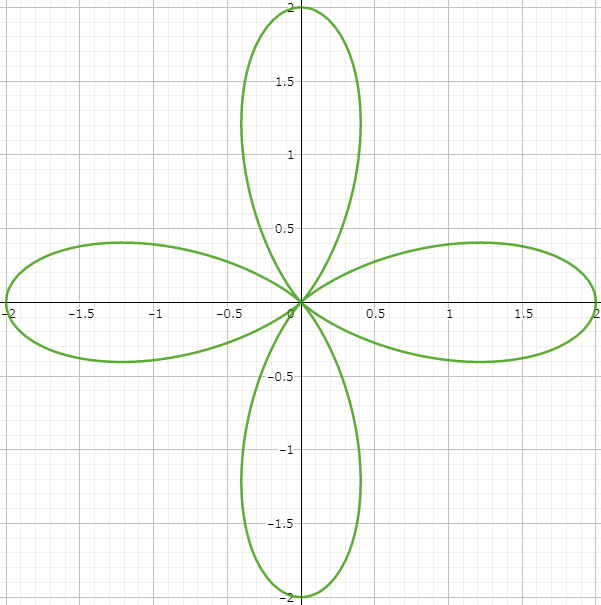
Notice the pattern? Change 3θ to 4θ and you jump from three to four leaves. Experiment with 2θ or 5θ, and watch the patterns evolve. For fun, see what 60θ reveals:
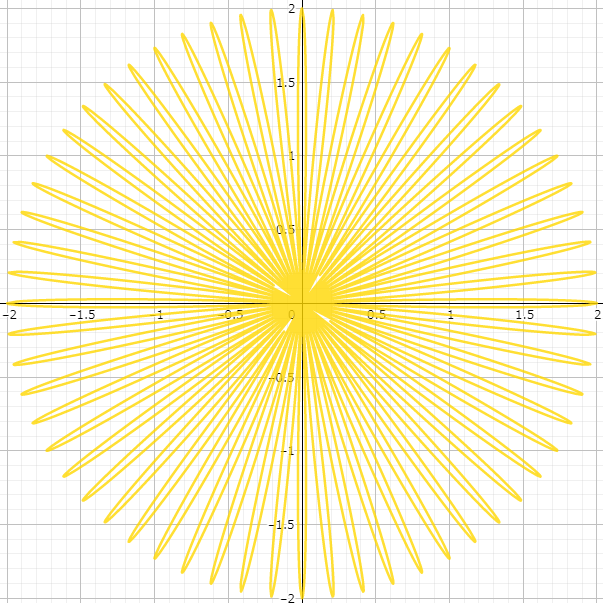
A burst of petals!
Star Equation
Lastly, reach for the stars with:
\(x^{\frac{2}{3}}+y^{\frac{2}{3}}=1\)
And its graph:
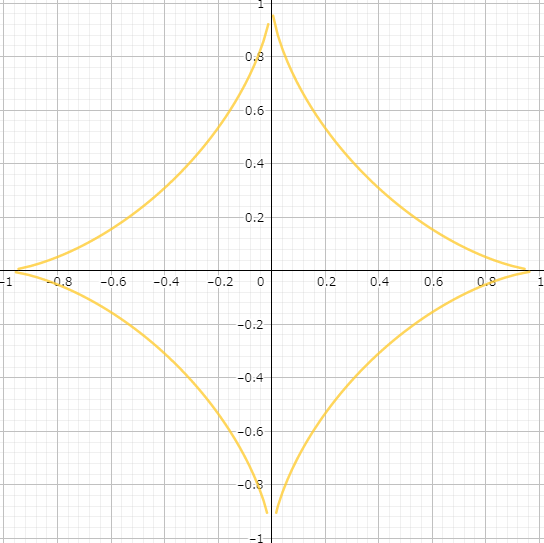
This one’s called the asteroid curve, truly a stellar pattern.