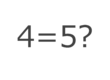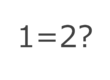Ever heard of the Monty Hall problem that caused a nationwide stir when it was showcased on TV in the 1960s? Dive into this article, and by the end, you’ll easily grasp the solution to one of the most famous paradoxes out there.
What’s the Monty Hall Problem?
Let’s kick things off with the basics of the Monty Hall problem.
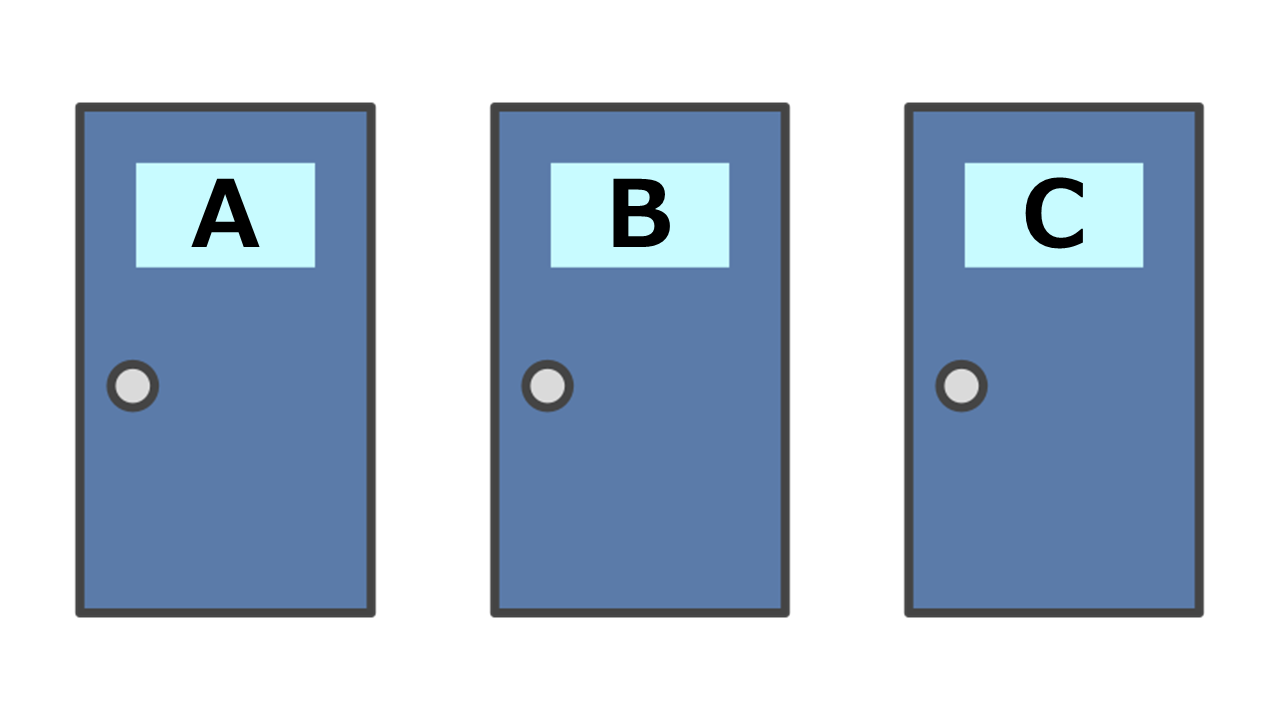
Imagine you’re faced with three doors. Behind one is a prize, and behind the other two – zilch. Let’s say you go with Door A. But then, Door B is opened to reveal no prize. You’re then offered a chance to stick with Door A or switch to Door C. Would changing your choice increase or decrease your odds of winning?
This is the essence of the Monty Hall problem. Knowing Door B has no prize, it seems like the odds of the prize being behind Door A or C are 50-50, right?
Well, here’s the counterintuitive solution:
- Chance that Door A hides the prize: 1/3
- Chance that Door C hides the prize:2/3
Seems hard to believe? Let’s dive deeper and clear things up in just a couple of minutes.
Unpacking the Monty Hall Problem
Initially, the odds of striking gold behind Doors A, B, or C are all the same – 1/3.
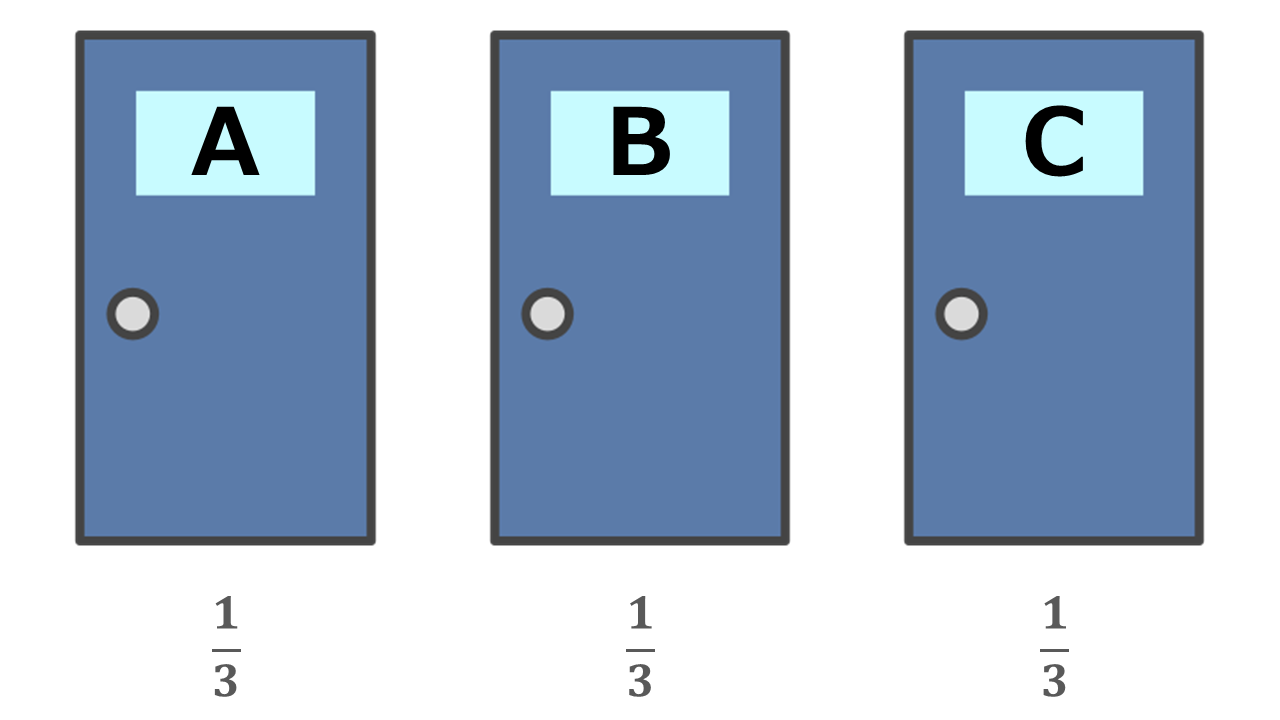
Here’s the breakdown if you initially pick Door A:
- Chance that Door A (highlighted in blue) has the prize: 1/3
- Chance that either Door B or C (highlighted in red) has the prize: 2/3
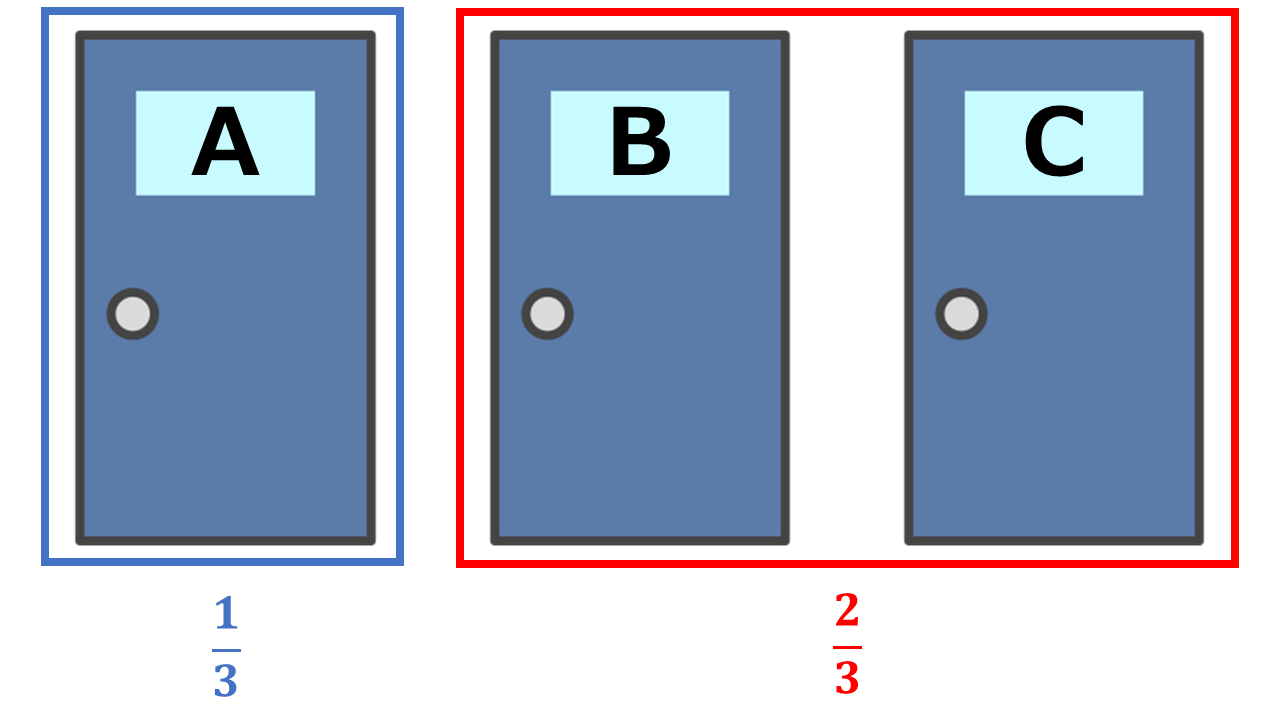
Now, which color frame, blue or red, gives you better odds? Picking the blue frame gives you a 1/3 chance of winning. But if you opt for the red frame, you get a 2/3 chance. There’s a catch, though. Since there are two doors in the red frame, you need to make another 1/2 choice. Hence, the actual odds when going for red end up being:
\(\displaystyle \frac{2}{3}×\frac{1}{2}=\frac{1}{3}\)
Up to this point, whether you stick with blue or switch to red, your chances seem equal. But what happens when you learn Door B is a dud? The odds for each frame remain. The blue still has a 1/3 chance, while the red frame has a 2/3 chance.
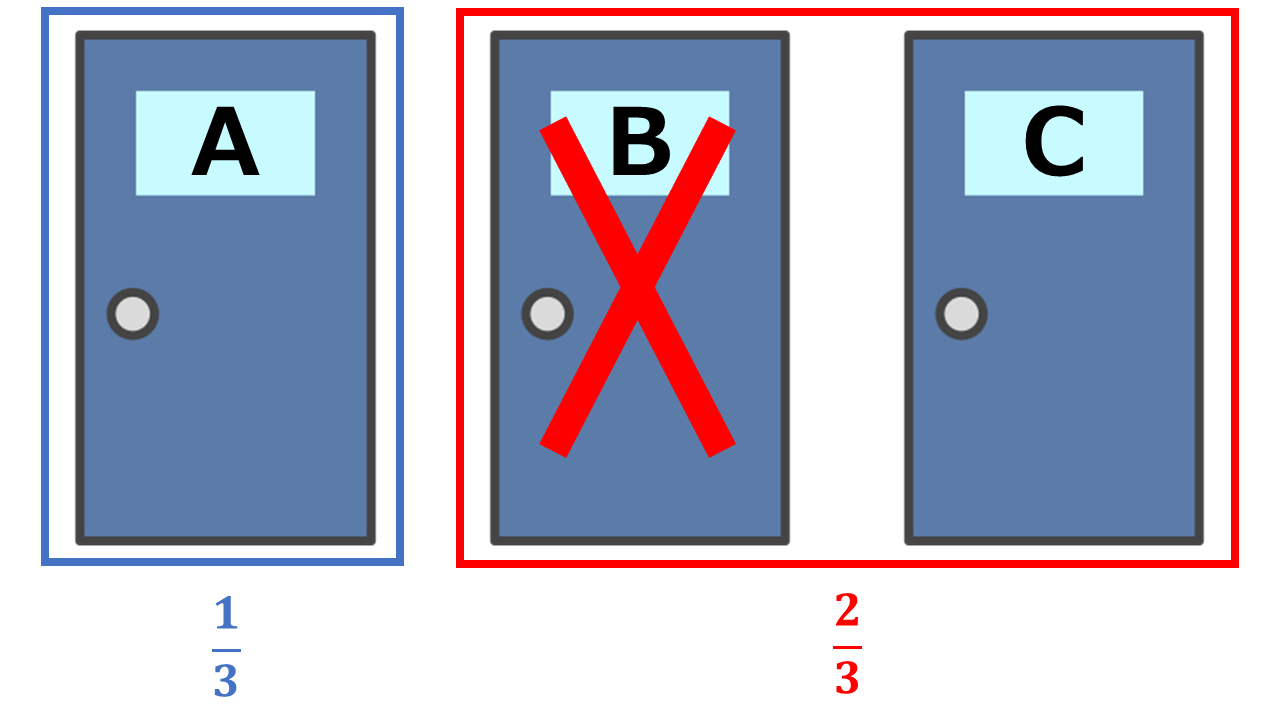
So, which should you choose? Sticking with the blue frame (Door A), the odds remain 1/3. But by choosing the red frame (now only Door C), the odds jump up to 2/3, especially since there’s no more 1/2 choice to make.
In essence, when you know Door B isn’t the winner, picking the red frame or Door C is the same thing. And that, my friends, is the Monty Hall problem in a nutshell, making more sense when framed this way!