Have you ever heard the claim that folding a newspaper 42 times can make it reach the moon? Most of you might be thinking, No way! But it’s a mind-blowing truth, and in this article, we’ll dive into the magic of exponential growth.
The Astonishing Truth: Folding a Newspaper 42 Times Reaches the Moon
Let’s start by proving the claim. Assuming the thickness of a newspaper is 0.1mm, if you fold it 42 times, its height would be:
\(\displaystyle 0.1×2^{42}=439804651110.4\)
Understanding the Growth
Want to see how the thickness grows with each fold? Here’s a breakdown:
| Folds | Thickness (in meters) | Notes |
|---|---|---|
| 1 | 0.000 | – |
| 2 | 0.000 | – |
| 3 | 0.001 | – |
| 4 | 0.002 | – |
| 5 | 0.003 | – |
| 6 | 0.006 | – |
| 7 | 0.013 | – |
| 8 | 0.026 | – |
| 9 | 0.051 | – |
| 10 | 0.10 | – |
| 11 | 0.20 | – |
| 12 | 0.41 | – |
| 13 | 0.82 | – |
| 14 | 1.64 | Equivalent to human height |
| 15 | 3.28 | – |
| 16 | 6.55 | – |
| 17 | 13 | – |
| 18 | 26 | – |
| 19 | 52 | – |
| 20 | 105 | – |
| 21 | 210 | – |
| 22 | 419 | Taller than Tokyo Tower (333m) |
| 23 | 839 | – |
| 24 | 1,678 | – |
| 25 | 3,355 | – |
| 26 | 6,711 | Higher than Mount Fuji (3,776m) |
| 27 | 13,422 | Surpasses Mount Everest (8,849m) |
| 28 | 26,844 | – |
| 29 | 53,687 | – |
| 30 | 107,374 | – |
| 31 | 214,748 | – |
| 32 | 429,497 | Beyond the altitude of Himawari satellite |
| 33 | 858,993 | – |
| 34 | 1,717,987 | – |
| 35 | 3,435,974 | – |
| 36 | 6,871,948 | – |
| 37 | 13,743,895 | – |
| 38 | 27,487,791 | – |
| 39 | 54,975,581 | – |
| 40 | 109,951,163 | – |
| 41 | 219,902,326 | – |
| 42 | 439,804,651 | Reaches the moon |
And visually, the growth looks something like this:
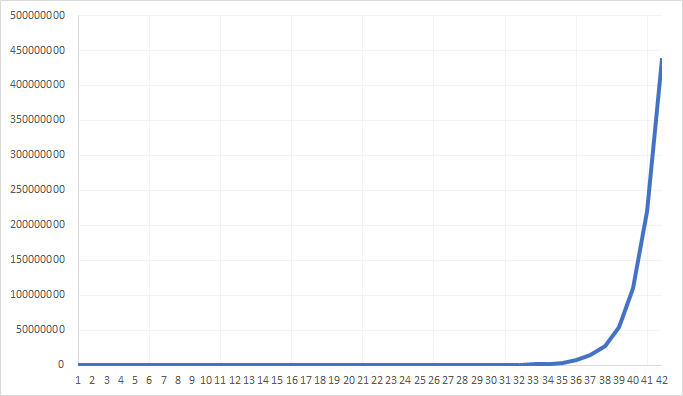
As you can see, as the number of folds increases, the thickness explodes.
Another Jaw-Dropping Fact
So, we’ve seen that folding a newspaper 42 times gets us to the moon. But what happens if we fold it 101 times? Hold onto your hats: it would reach the edges of the universe.
How We Calculated It
The distance from the center to the edge of the universe is 13.8 billion light years. Given that 1 light year is approximately 9.5 trillion km, the radius of the universe can be found as:
\(\displaystyle 13,800,000,000×9,500,000,000,000=1.311×10^{23}\)
The radius of the universe is roughly 1.311×10^23 km. So, to figure out how many times we need to fold the newspaper to reach the universe’s edge (keeping our calculations in meters):
\begin{align}
0.1×10^{-3}×2^x&=1.311×10^{23}×10^3\\
2^x&=\frac{1.311×10^{23}×10^3}{0.1×10^{-3}}\\
2^x&=1.311×10^{30}\\
log_22^x&=log_2(1.311×10^{30})\\
xlog_22&=log_2(1.311×10^{30})\\
x&=\frac{log_2(1.311×10^{30})}{log_22}\\
x&=100.0485105＜101
\end{align}
With 101 folds, the newspaper’s thickness surpasses the universe’s radius. Meaning, if we imagine the universe as a sphere, a 101-folded newspaper would reach any point on the universe’s edge. The power of exponential growth is truly beyond our wildest imagination!
Discover Famous Math Theories: Intriguing Number Facts and Mathematics Tricks That Will Amaze You
You know how math classes in school can be kinda dull or even a pain for most folks, right? But get this, math is actually pretty fascinating. To prove how cool math can be, I’ve gathered some fun math stories for you! Even if you’re not a math fan, you’re gonna have a good time…
