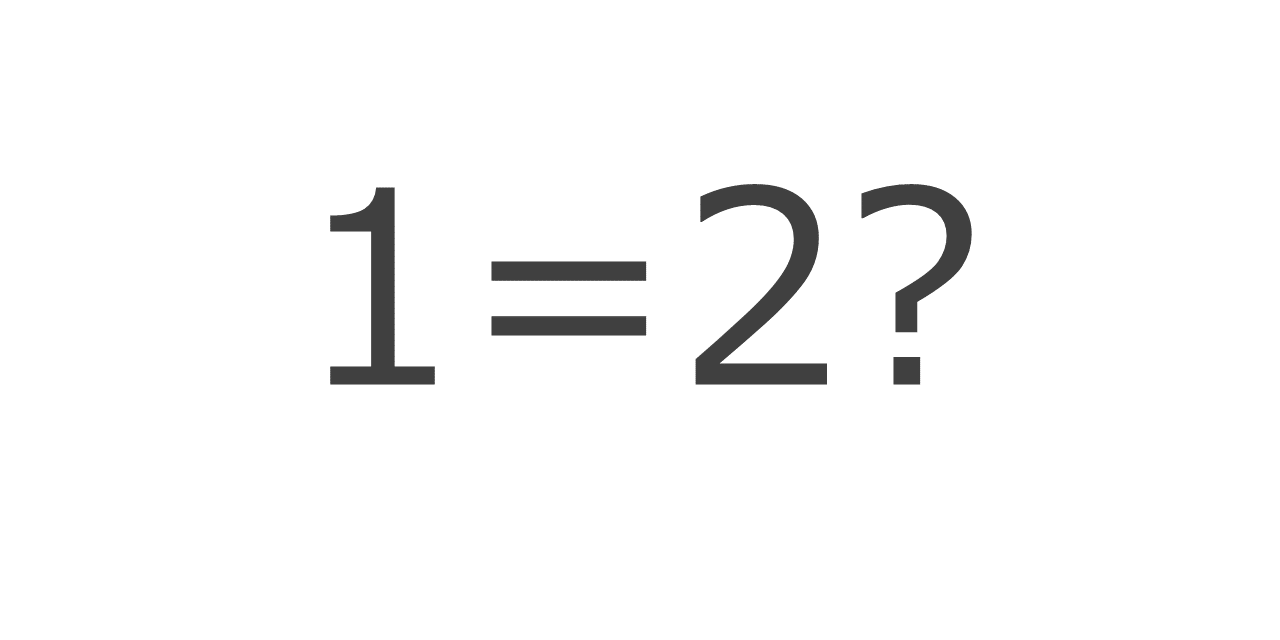Defining Paradox in Basic Math: The Mathematical Proof of 1=2 and the Intricacies that Define Mathematics

Ever thought 1 could equal 2? Well, at first glance, some proofs might have you believe it. But remember, 1 definitely doesn’t equal 2! So, there’s a sneaky mistake hiding somewhere in each proof. Ready to challenge yourself and find it?

Proving with Arithmetic

Let’s dive right into a classic arithmetic proof:

\(a=b\)
\(a^2=ab\)
\(a^2-b^2=ab-b^2\)
\((a-b)(a+b)=b(a-b)\)
\(a+b=b\)
\(a+a=a\)
\(2a=a\)
\(2=1\)

Wow, we seem to have just proved 1 = 2! But where did we go wrong?

Spotting the Mistake

Our error is right here:

\((a-b)(a+b)=b(a-b)\)
\(a+b=b\)

Since we began with \(a=b\), this means \(a-b=0\). And in math, dividing by zero is a big no-no! This is where the proof falls apart.

Proving with Triangles

Now, let’s use triangles for a visual treat. Imagine an equilateral triangle with each side measuring 1 unit.

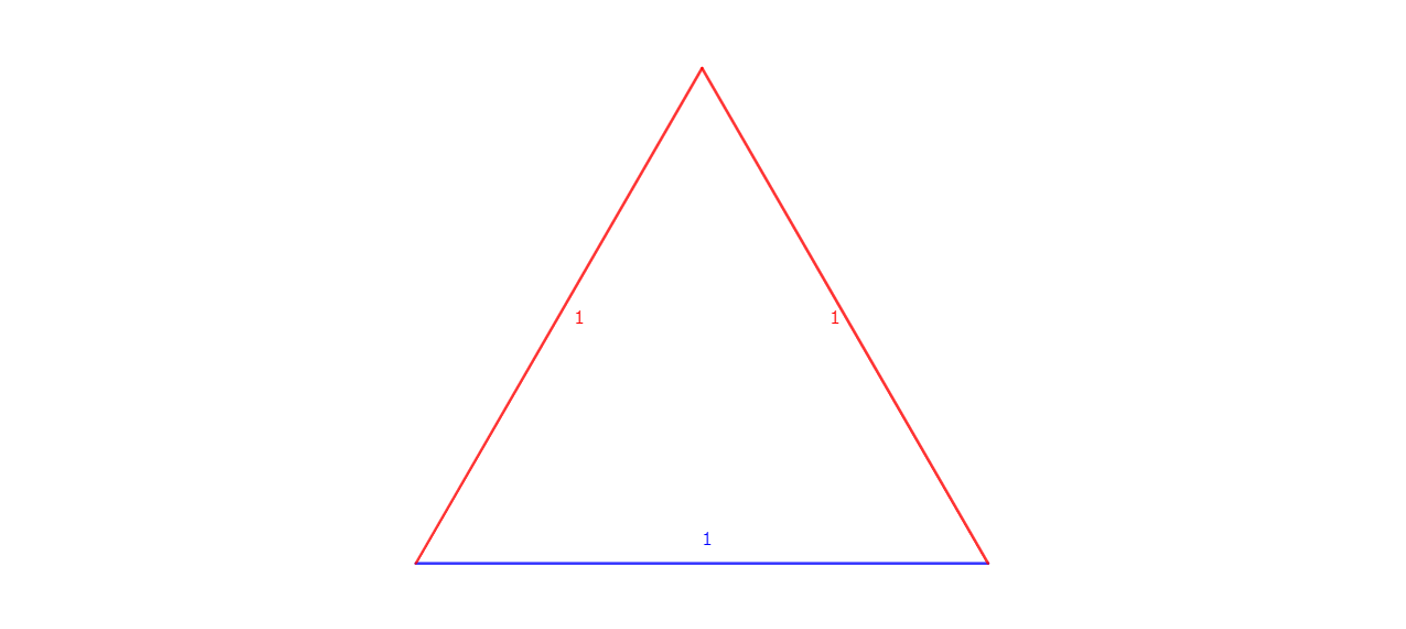
When you split this triangle, the base remains 1 unit, while the sum of the other sides remains 2.

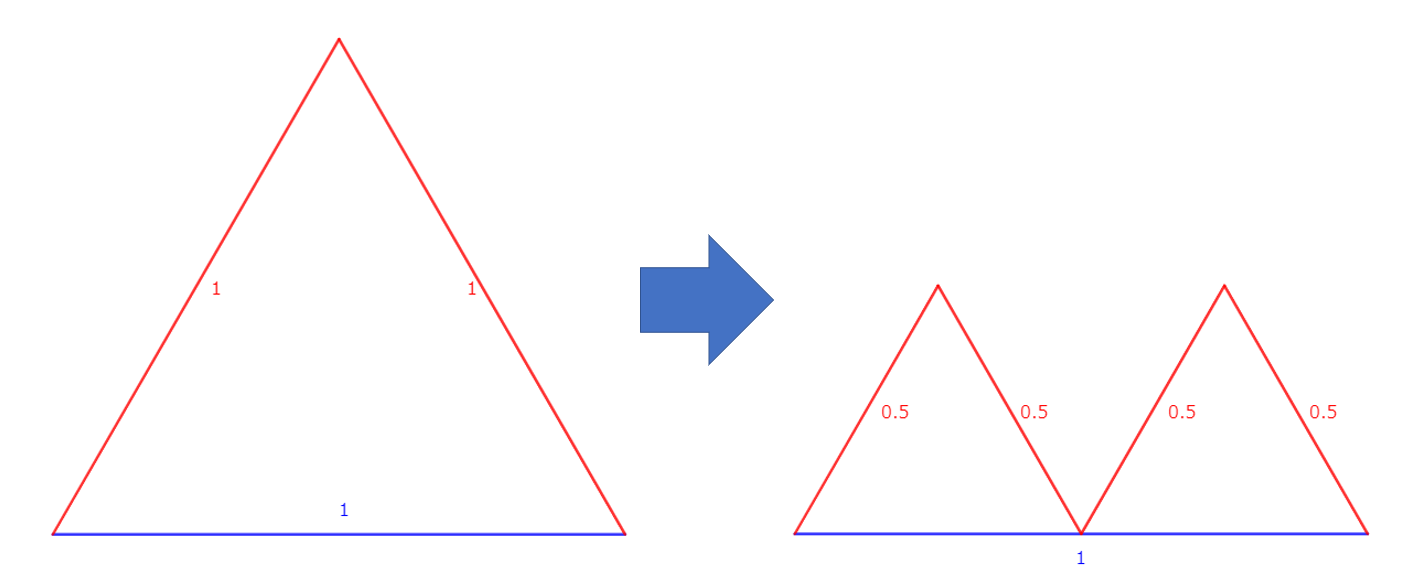
Keep on dividing, and it seems the sum of those sides will eventually equal the base!

Based on this, it appears 1=2. But what went wrong this time?

Spotting the Mistake

It’s simple. No matter how tiny, a triangle is still a triangle. Those sides will never truly become a straight line. Don’t be fooled!

Proving with Differentiation

Next, let’s venture into calculus.

When you square the number 3, it means you have three 3s:

\(\displaystyle3^2=\underbrace{3+3+3}_{3}\)

Now, replace 3 with a variable \(x\):

\(\displaystyle x^2=\underbrace{x+x+x…x}_{x}\)

Differentiating both sides, we get:

\(2x=\underbrace{1+1+1…1}_{x}\)
\(2x=x\)
\(2=1\)

Once again, it looks like we’ve proved 1=2. What’s the catch here?

Spotting the Mistake

The sum of \(x\) added \(x\) times is:

\(\displaystyle \underbrace{x+x+x…+x}_{x}=\sum_1^xx\)

But when differentiated, it’s not what we considered in our proof. The variable \(x\) atop the summation wasn’t differentiated. This is where the proof fumbles.

Proving with Series

Lastly, let’s dive into a tricky series proof. A series is the sum of a sequence of numbers following a particular rule.

Consider this alternating series:

\(\displaystyle X=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}…\)

Now, rearrange the terms:

\(\displaystyle X=(1-\frac{1}{2})-\frac{1}{4}+(\frac{1}{3}-\frac{1}{6})-\frac{1}{8}+(\frac{1}{5}-\frac{1}{10})…\)
\(\displaystyle X=(\frac{2}{2}-\frac{1}{2})-\frac{1}{4}+(\frac{2}{6}-\frac{1}{6})-\frac{1}{8}+(\frac{2}{10}-\frac{1}{10})…\)
\(\displaystyle X=\frac{1}{2}-\frac{1}{4}+\frac{1}{6}-\frac{1}{8}+\frac{1}{10}…\)
\(\displaystyle X=\frac{1}{2}(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}…)\)
\(\displaystyle X=\frac{1}{2}X\)
\(\displaystyle 2X=X\)
\(\displaystyle 2=1\)

Guess what, we ended up with 1=2 again. Can you unravel this puzzle?

Spotting the Mistake

The catch is in the definition of a series. It’s an ordered sum of numbers. Switching the order can affect the sum, especially in the case of series like this one where the absolute sum diverges. The absolute value of our series, where everything is positive, is infinite. So, switching orders in such cases? A big mistake.

While 1=2 is a fun illusion, did you know 0.99999… really does equal 1? Intrigued? Dive into this topic in another article.