Ever Wondered How Far the Horizon Is? Here’s a Fun Way to Find Out!

Hey folks! Ever looked out into the vastness and wondered just how far that horizon line really is? Believe it or not, there’s a simple math trick from middle school trigonometry that can help you crack the code. Take a wild guess before reading on. Is the horizon closer than we think, or way off in the distance? Have a little fun and take a guess!

Cracking the Horizon Mystery

So, how far do you reckon the horizon is? Before diving into the calculations, what’s your guess? For the record, I pegged it around 100km.

How to Do the Math

Alright, time to unveil the secret formula. Let’s define the parameters we need:

• Earth’s Radius:\(R\)
• Viewer’s Height:\(h\)
• Distance to the Horizon:\(x\)

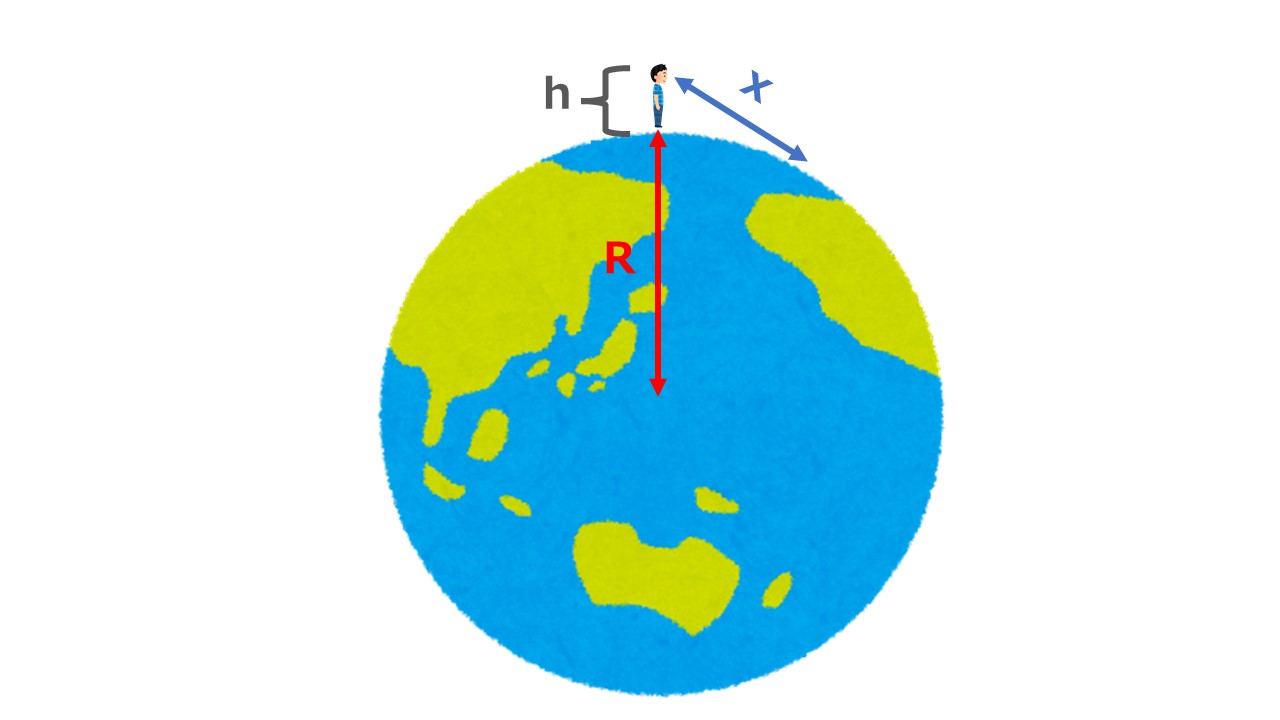
As shown in the illustration, the line representing the distance /(x/) to the horizon forms a right angle with a radius /(R’/) (because it acts as a tangent).

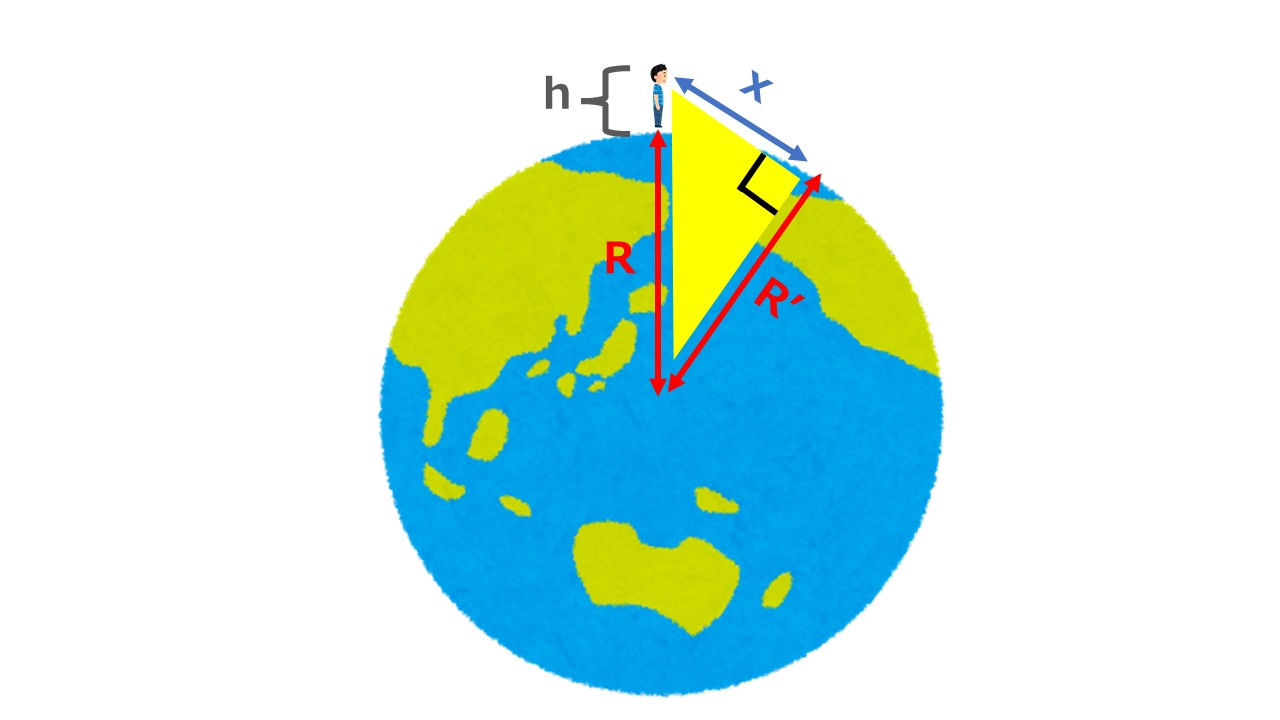
Given that we have a right triangle, good old Pythagoras gives us:

\(x^2+R’^2=(R+h)^2\)
\(x^2=(R+h)^2-R’^2\)
\(x= \sqrt{(R+h)^2-R’^2}\)
Note: The distance to the horizon \(x\) is always positive.

The Result

Punching in the numbers, we’ve got the Earth’s radius as about 6378km. Let’s assume an average person’s height is 150cm:

\(\displaystyle x= \sqrt{(6378+ \frac{150}{100×1000})^2-6378^2}\)
\(x\)≒ 4.37km

Surprised? That’s just about 4.37km! Closer than you thought, right?

Does Height Really Matter?

We worked with a height of 150cm for our example. But how does the distance change with height? Check out this cool table:

For someone 100cm tall, a person who’s 200cm tall will see the horizon at a distance that’s 1.4 times further. So, if you ever find yourself stranded on a deserted island, maybe ask the tallest person to scout for rescue ships.